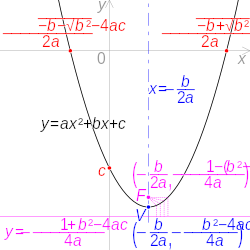
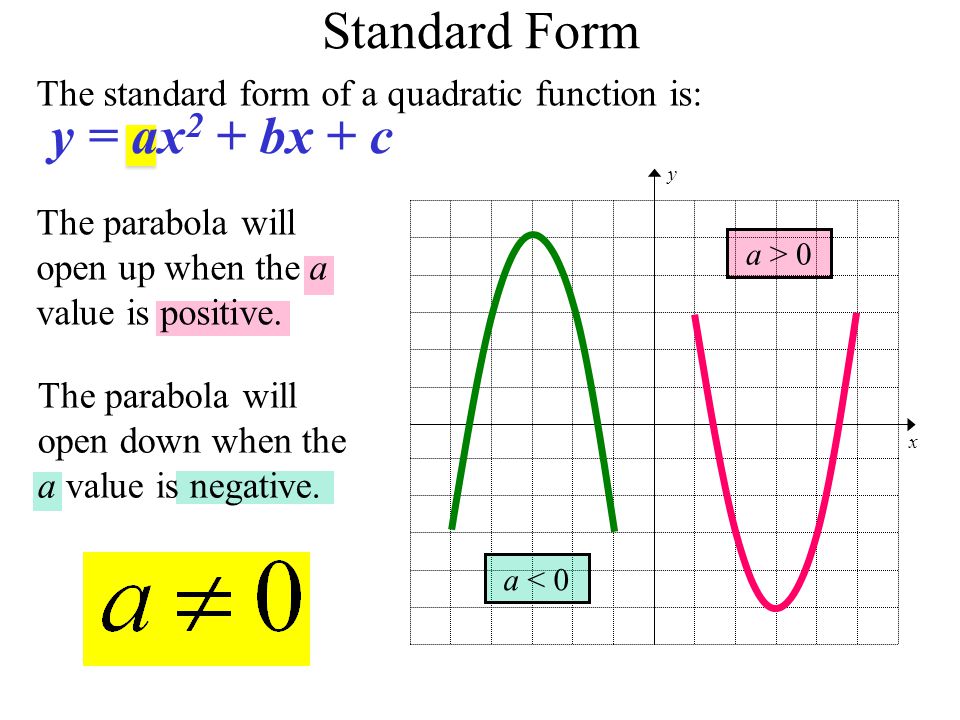
Yax2+bx+c What Is A B And C
The parabola is rotated 180° about its vertex (orange).

Yax2+bx+c what is a b and c. A + b + c = 1 D. The y-intercept of the equation is c. How to Find the Vertex y = ax2 + bx + c The vertex has an x coordinate of –b/2a To find the y coordinate one must place the x coordinate number into the places x occupies in the problem.
Rewrite the equation as. B = B. The exception to it not being used as a vertex is when the b is equal to 0.
12 = a(-1)^2 + b(-1) + c" 2" Point (-3, 12):. Suppose that we have an equation y=ax^2+bx+c whose graph is a parabola with vertex (3,2), vertical axis of symmetry, and contains the point (1,0). Interactive Quadratic Function Graph.
The graph of y=ax^2+bx+x is given below, where a,b, and c are integers. The effects of variables a and c are quite straightforward, but what does variable b do?. Use the 3 points to write 3 equations and then solve them using an augmented matrix.
The velocity is the slope of the 1st equation. I'm dealing with quadratic equations (y=ax2+bx+c) and I need to know what the three variables, a, b and c stand for. The velocity is the derivative of this equation.
Find the parabola {eq}y = ax^2 + bx + c {/eq} passing through the points ( -1, 9), (1, -1), and (2, 3). Stack Exchange network consists of 176 Q&A communities including Stack Overflow, the largest, most trusted online community for developers to learn, share their knowledge, and build their careers. This equation can also be factored to the form:`y.
So m = 2A. Explorations of the graph. If you don't, you might use the wrong values for a, b, or c, and then the formula will give incorrect solutions.
We have split it up into three parts:. Suppose you have ax 2 + bx + c = y, and you are told to plug zero in for y.The corresponding x-values are the x-intercepts of the graph. So in this case:.
(25 points) Short Answer Find a, b, and C such that the parabola y=ax^2+bx+c passes thru the three points (1,3), (2,3), and (3,5). If three points of the parabola are given, substitute the points to the. Dy/dx = v = 2Ax +B.
Calculus Single Variable Calculus Find a parabola y = ax 2 + bx + c that passes through the point (1, 4) and whose tangent lines at x = −1 and x = 5 have slopes 6 and −2, respectively. Find a parabola y = ax 2 + bx + c that passes through the point (1, 4) and whose tangent lines at x = −1 and x = 5 have slopes 6 and −2, respectively. The X and the y coordinates of a projectile launched from the origin as a function of time are given by X=Vot and Y=Vot-1/2gt^2 whre Vox and Voy are the components of initial velocity.
A - b = 1 B. Irspow +6 ocabanga44 and 6 others learned from this answer. In the following applet, you can explore what the a, b, and c variables do to the parabolic curve.
Roots and y-intercept in red;. Then the equation a x 2 + b x + c = 0 ax^2+ bx + c = 0 a x 2 + b x + c = 0 is bound to have two roots since it is a quadratic equation. Look up the formula if you don't know it already.
Parabola and Linear Equations:. Most of us are aware that the quadratic equation yields the graph of a parabola. Move to the left side of the equation by subtracting it from both sides.
The following graphs are two typical parabolas their x-intercepts are marked by red dots, their y-intercepts are marked by a pink dot, and the vertex of each parabola is marked by a green dot:. When you want to graph a quadratic function you begin by making a table of values for some values of your function and then plot those values in a coordinate plane and draw a smooth curve through the points. The minimum / maximum point of the quadratic equation is given by the formula:.
Before solving a quadratic equation using the Quadratic Formula, it's vital that you be sure the equation is in this form. They are where the graph crosses the x-axis, or simply put, where y = 0. What must be true of the pivots of the augmented matrix A|b) if the system is to have a unique solution?.
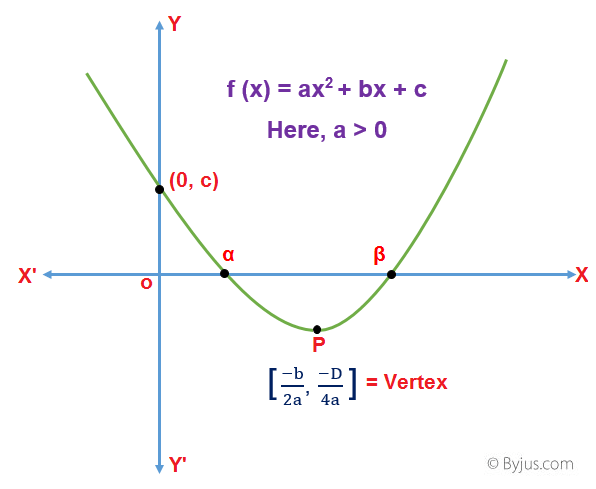
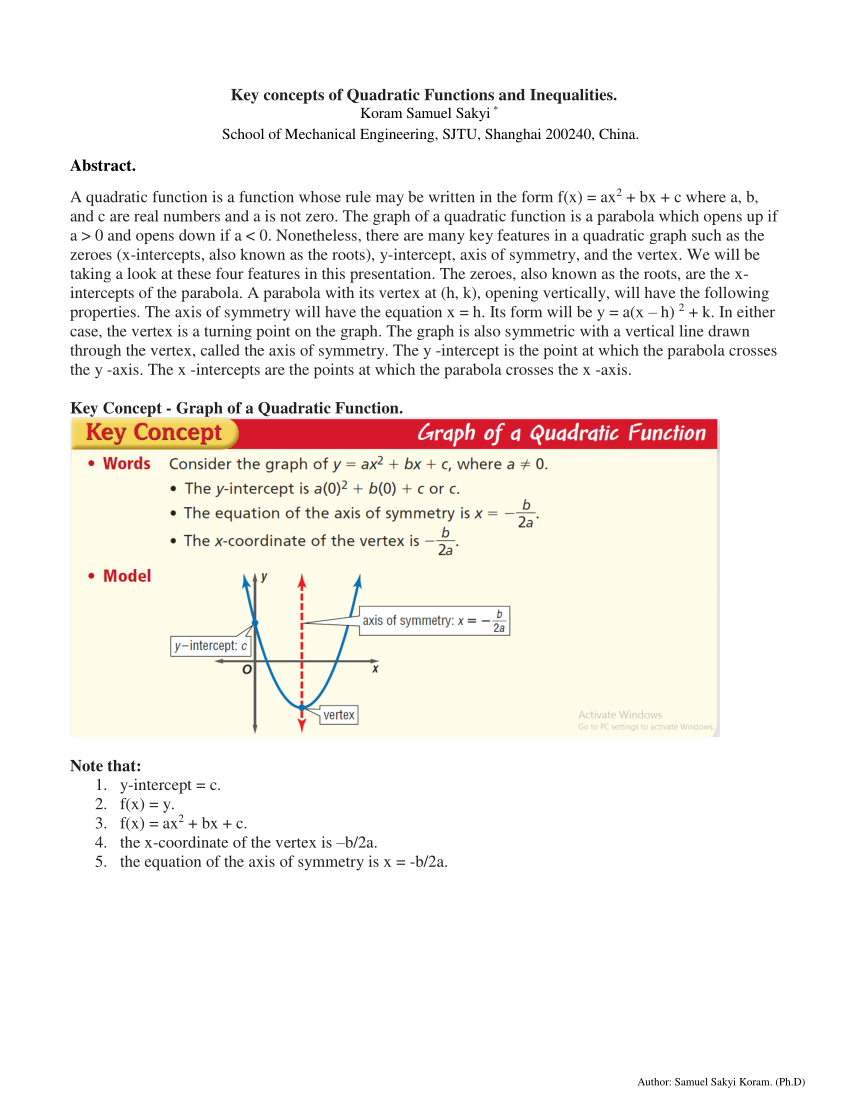
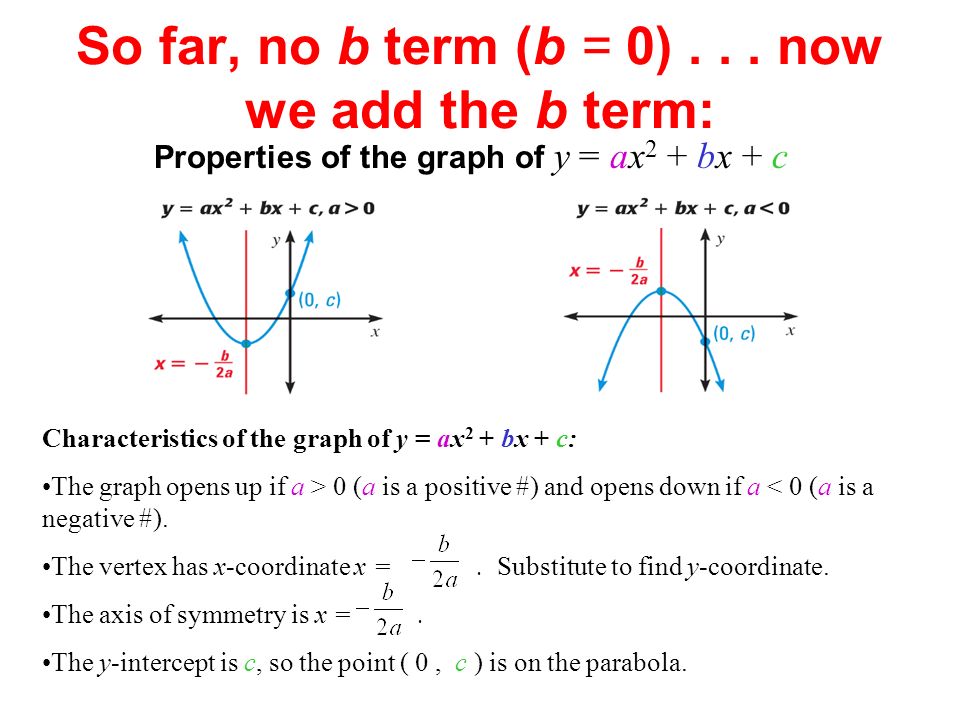
In the previous section, The Graph of the Quadratic Function, we learned the graph of a quadratic equation in general form y = ax 2 + bx + c. Curve is crossing x-axis at two points ⇒ roots are real ⇒ b 2 − 4 a c > 0 Roots are of opposite signs c / a < 0 ⇒ c < 0 Also magnitude of +ve root is larger ⇒ sum of roots > 0 ⇒ − b / a > 0 ⇒ b < 0 Hence all the options are correct. Yes, we can find it using infinitesimals.
A) touches the x-axis at 4 and passes through (2,12). Will find the roots, or zeroes, of the equation. Let f(x) = ax^2+bx+c Then the slope at x is the standard part of:.
` ` `y=ax^2 + bx +c`is the original function for a parabola. From the 2nd equation, we know that c=1. M = 2A is the acceleration ( constant acceleration (that is the acceleration does not.
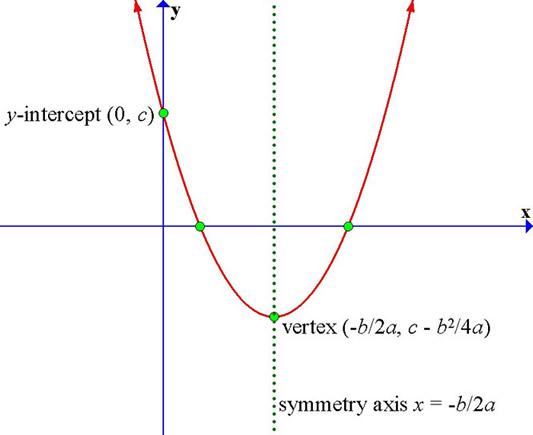
Y = ax 2 + bx + c:. It’s formula is (0, c). I'm pretty sure c is the y-intercept, and I think b is used to partially calculate the turning point.
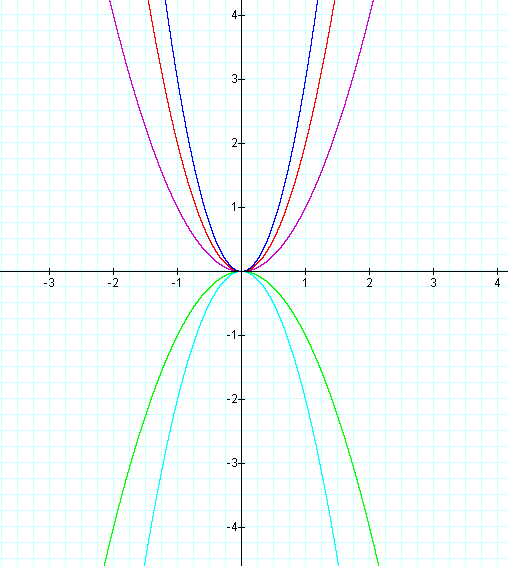
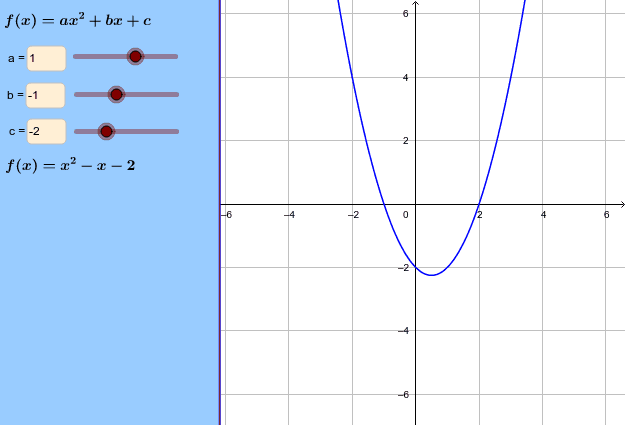
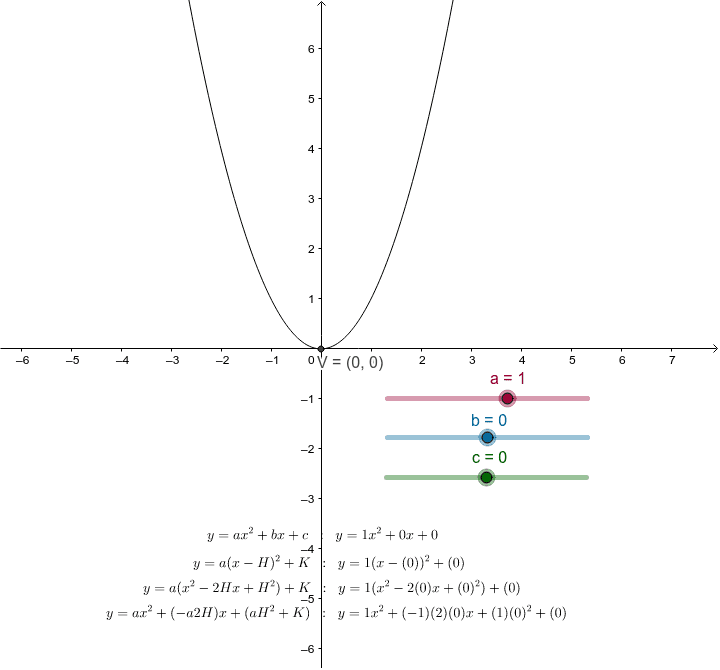
We are going to explore how each of the variables a, b, and c affect the graph of .First, let's take a look at the simplest of the quadratic equation , where a = 1, b = 0, and c = 0. Solve by using the quadratic formula. Standard form of parabola is y = ax 2 + bx + c.
Find a, b, c. Bingo hows the castigation. So solving ax 2 + bx + c = 0 for x means, among other things, that you are trying to find x-intercepts.Since there were two solutions for x 2 + 3x – 4 = 0, there must then be two x-intercepts on the graph.Graphing, we get the curve below:.
Then make 5 and -5 as the points where it intersects the x- axis. The roots of a quadratic function are the same as its zeroes. Substitute the 3 points, (1, -4), (-1, 12), and (-3, 12) into and make 3 linear equations where the variables are a, b, and c:.
Substitute the values , , and into the quadratic formula and solve for. Vertex form of parabola is y = a(x-h) 2 + k where (h,k) is the vertex. Solve for x y=ax^2+bx+c.
Well make the turning point or the vertex is 0, 10 and thatbis the point where dy/ dx =0. These two solutions may or may not be distinct, and they may or may not be real. The form ax 2 + bx + c = 0 is called standard form of a quadratic equation.
We multiply quantities of different units (eg. If c is repreatedly increased by one to create new functions, how are the graphs of the functions the same or different?. You get that by rewriting the equation in the standard form ax^2 + bx + c = 0 , where a, b, and c are constants.
In particular, we will examine what happens to the graph as we fix 2 of the values for a, b, or c, and vary the third. The letters a, b and c stand for the co-efficients. The curve y=ax^2 + bx + c passes through the point (2,8) and is tangent to the line y=2x at the orgin.
15=4a+2b+c 15=4a+2b+1 14=4a+2b. So substitute the value into the 1st and 3rd equations. Plug those values in to the equation y = x^2 + x + c and you'll get the same equation as you've been given.
Let epsilon denote an infinitesimal. Find in the form y= ax^2 + bx +c, the equation of the quadratic whose graph:. Find b and c so that y= 10x 2 +bx+c has vertex (5,-4).
B = B is the initial velocity of the car at x = 0. A) touches the x-axis at 4 and passes through (2,12) b) has vertex (-4,1) and passes through (1,11) Answer provided by our tutors y= ax^2 + bx +c. A is the same in each equation, which is given as 10, and if we also plug in the vertex given we get (in vertex form).
Y=ax 2 +bx+c (-3,10) 10=a(-3) 2 +b(-3)+c 10=9a-3b+c (0,1) 1=a(0) 2 +b(0)+c 1=c (2,15) 15=a(2) 2 +b(2)+c 15=4a+2b+c. Interactive lesson on the graph of y = ax² + bx + c, including its axis of symmetry and vertex, and rewriting the equation in vertex form. Use the quadratic formula to find the solutions.
If Y = Ax^2 + Bx +C is the position of the car. Hence, k = 3. Solution for The curve y = ax2 + bx + c passes through the point (1, 2) and is tangent to the line y = x at the origin.
1 See answer Answer 5.0 /5 5. Suppose we have a parabola y = a x 2 + b x + c y = ax^2+ bx + c y = a x 2 + b x + c. The graph of y=ax^2+bx+c is translated by the vector (4 5).The resulting graph is y=2x^2-13x+21.Find the values of a,b and c.
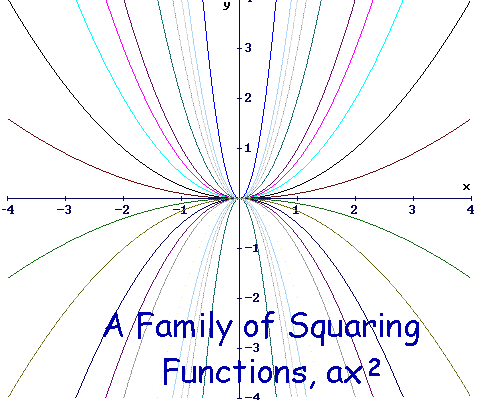
What is (a, b, c)?. Plots of quadratic function y = ax2 + bx + c, varying each coefficient separately while the other coefficients are fixed (at values a = 1, b = 0, c = 0) A quadratic equation with real or complex coefficients has two solutions, called roots. Find a, b, and c.
Make room on the left-hand side, and put a copy of "a" in front of this space. To get foot-pounds) and divde quantities of. A - b + c = 1 Answer by ikleyn() (Show Source):.
Y = ax 2 + bx + c In this exercise, we will be exploring parabolic graphs of the form y = ax 2 + bx + c, where a, b, and c are rational numbers. The equation of a parabola is a quadratic equation in the form ax2+bx+c = y a x 2 + b x + c = y, where a,b,c ∈R a, b, c ∈ R. So 2Ax + B = mx +b.
I had to solve this quadratic equation using the complete the square method. Y – c = ax 2 + bx:. The quadratic equation itself is (standard form) ax^2 + bx + c = 0 where:.
A quadratic function can have 0, 1, or 2 roots. In this case a = 3, b = -11 and c = -4. Answer is a=1, b=2, c=0.
XXxTenTacion Jul 16, 18. Graph of y = ax 2 + bx + c, where a and the discriminant b 2 − 4ac are positive, with. 12 = a(-3)^2 + b(-3) + c" 3" You have 3 equations with 3 unknown values, a.
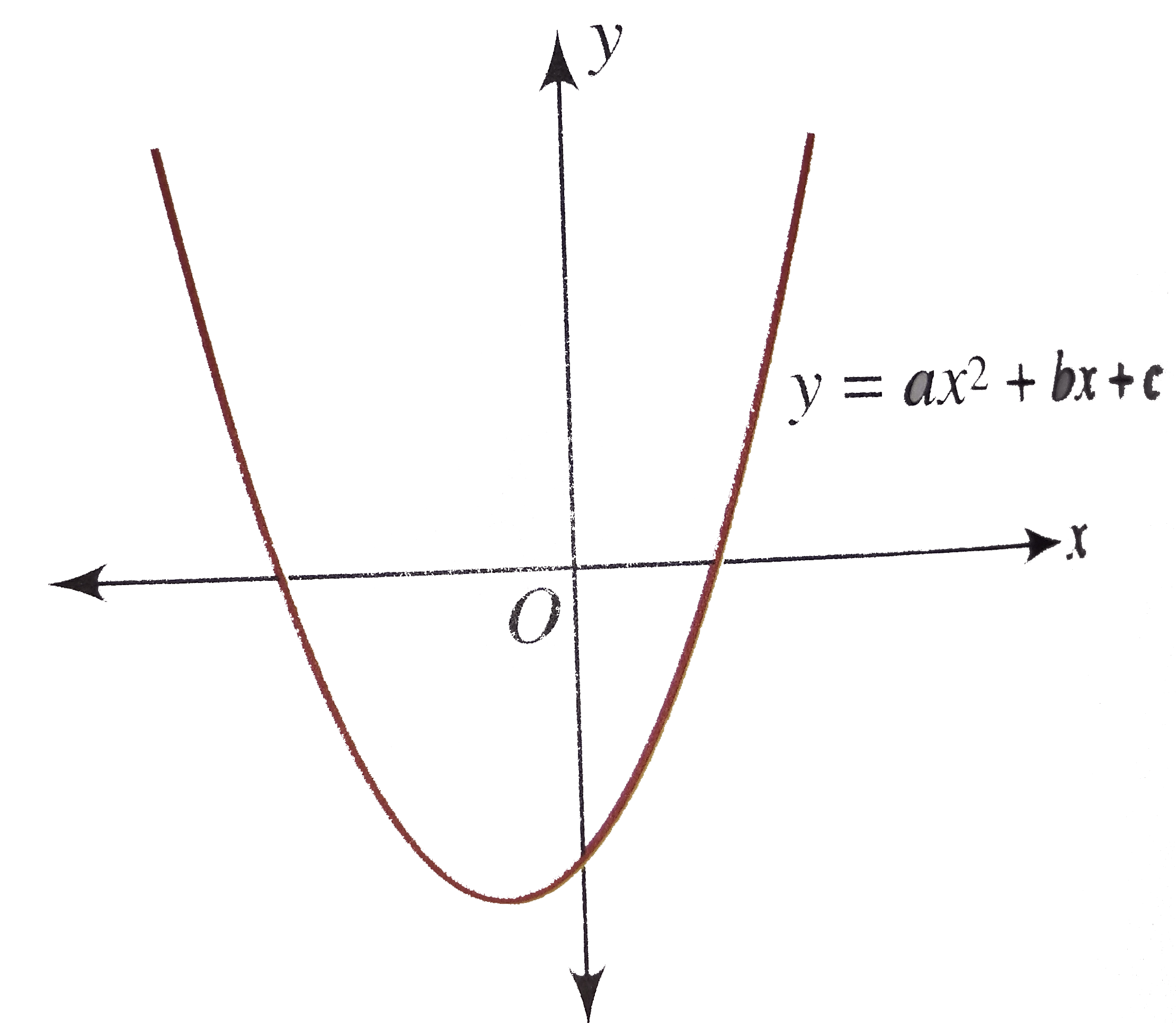
The graph of a quadratic equation in two variables (y = ax2 + bx + c) is called a parabola. Hi Debbie, The point here is that you can only add quantities that have the same units. Factor out whatever is multiplied on the squared term.
A quadratic function is in the form of y=ax^2+bx+c. In mathematical geometry, a parabola is a part of the conic. However, the number of real roots depends on the parabola.
Similar to the earlier sections in this chapter, we are going to apply trinomial factoring to reverse the process of FOIL to solve the problems. We can find the slope using infinitesimals. The equation of a parabola is y=ax^2+bx+c, where a, b, c are constants.
Visualisation of the complex roots of y = ax 2 + bx + c:. The general equation for a parabola is y = ax 2 + bx + c, where a, b, c are constants. Move the loose number over to the other side.
You can change the shape and location of this by increasing the a, b, and c values. The graph is a parabola and hence has an equation y = k(x - v)^2 + h, where (v,h) are the coordinates of the vertex. In this section, we will learn how to find all the possible answers to the unknown "b" in the polynomials a x 2 + b x + c {ax^2 + bx+c} a x 2 + b x + c.
Hence, your parabola is y = k(x - 5)^2 - 3. X =-b ± b 2-4 a c 2 a. Vertex and axis of symmetry in blue;.
(f(x+epsilon) - f(x))/((x+epsilon) - x) = ((a(x+epsilon)^2+b(x+epsilon)+c)-(ax^2+bx+c))/epsilon = ((a(x^2+2epsilonx+epsilon^2)+b(x+epsilon)+c)-(ax^2+bx+c))/epsilon = ((ax^2+(b+2epsilona)x+(c+bepsilon. What are the units of each constant if y and x are in meters?. But I'm not sure.
In the xy-plane, if the parabola with equation y = ax^2 + bx + c, where a,b,and c are constants, passes through the point (-1,1), which of the following must be true?. This gives us the quadratic equation. Stack Exchange network consists of 176 Q&A communities including Stack Overflow, the largest, most trusted online community for developers to learn, share their knowledge, and build their careers.
The c is always a constant. What would i do to solve this?. The Curvature of graph is given by the formula math{\displaystyle k={\frac {y''}{\left(1+y'^{2}\right)^{\frac {3}{2}}}}.}/math Here mathy = a x^2 + b x + c.
A is the coefficient of the x^2 term b is the coefficient of the x term c is the constant term you use the a,b,c terms in the quadratic formula to find the roots. For any quadratic equation of the form y = ax 2 + bx + c, the quadratic formula below. By Kristina Dunbar, UGA.
The graph passes through (4,0), hence, 0 = k(4 - 5)^2 - 3 and 0 = k - 3. Focus and directrix in pink;.
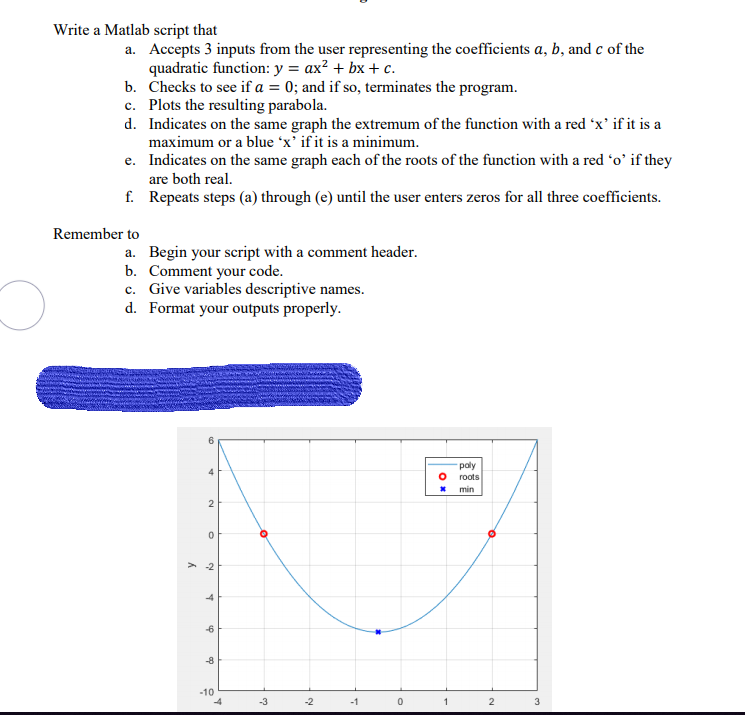
Solved Write A Matlab Script That Accepts 3 Inputs From T Chegg Com
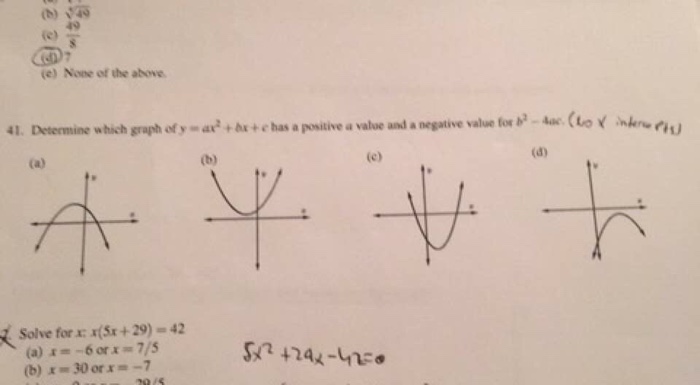
Solved Determine Which Graph Of Y Ax 2 Bx C Has A P Chegg Com

Solved A Quadratic Equation In The Form Y Ax 2 Bx C Chegg Com
Yax2+bx+c What Is A B And C のギャラリー

Differentiate Sin N Ax 2 Bx C Youtube
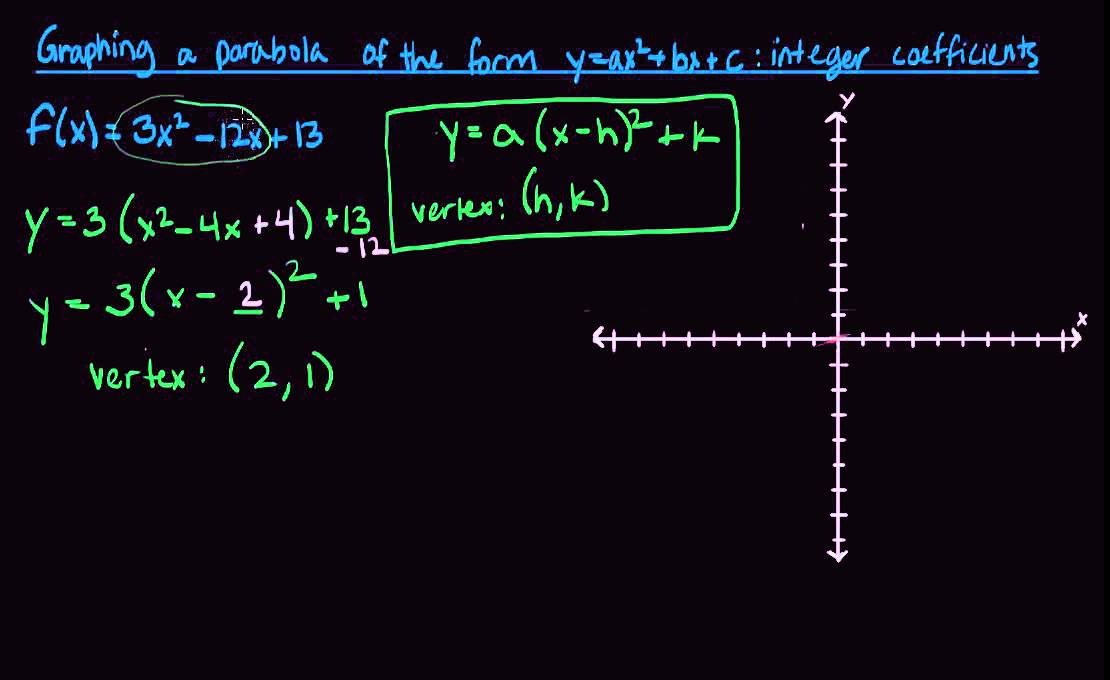
Graphing A Parabola Of The Form Y Ax2 Bx C With Integer Coefficients Youtube
Q Tbn 3aand9gcrj4zefjn32tclwxwszidmmbulqtnieycx Jyr6u1jhn9b002k8 Usqp Cau
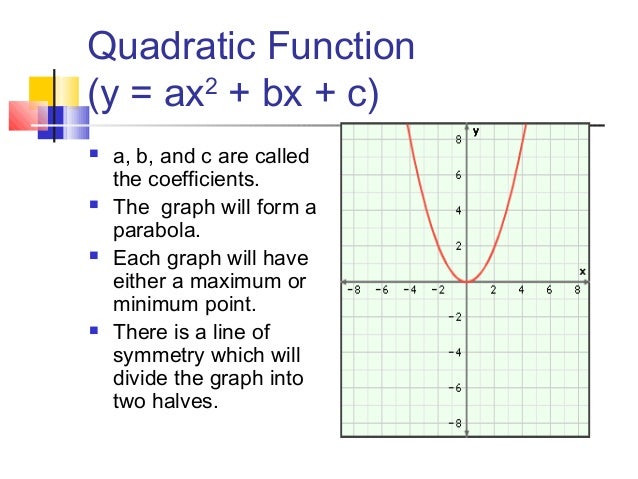
5 1 Quadratic Functions

Quadratic Function Wikipedia
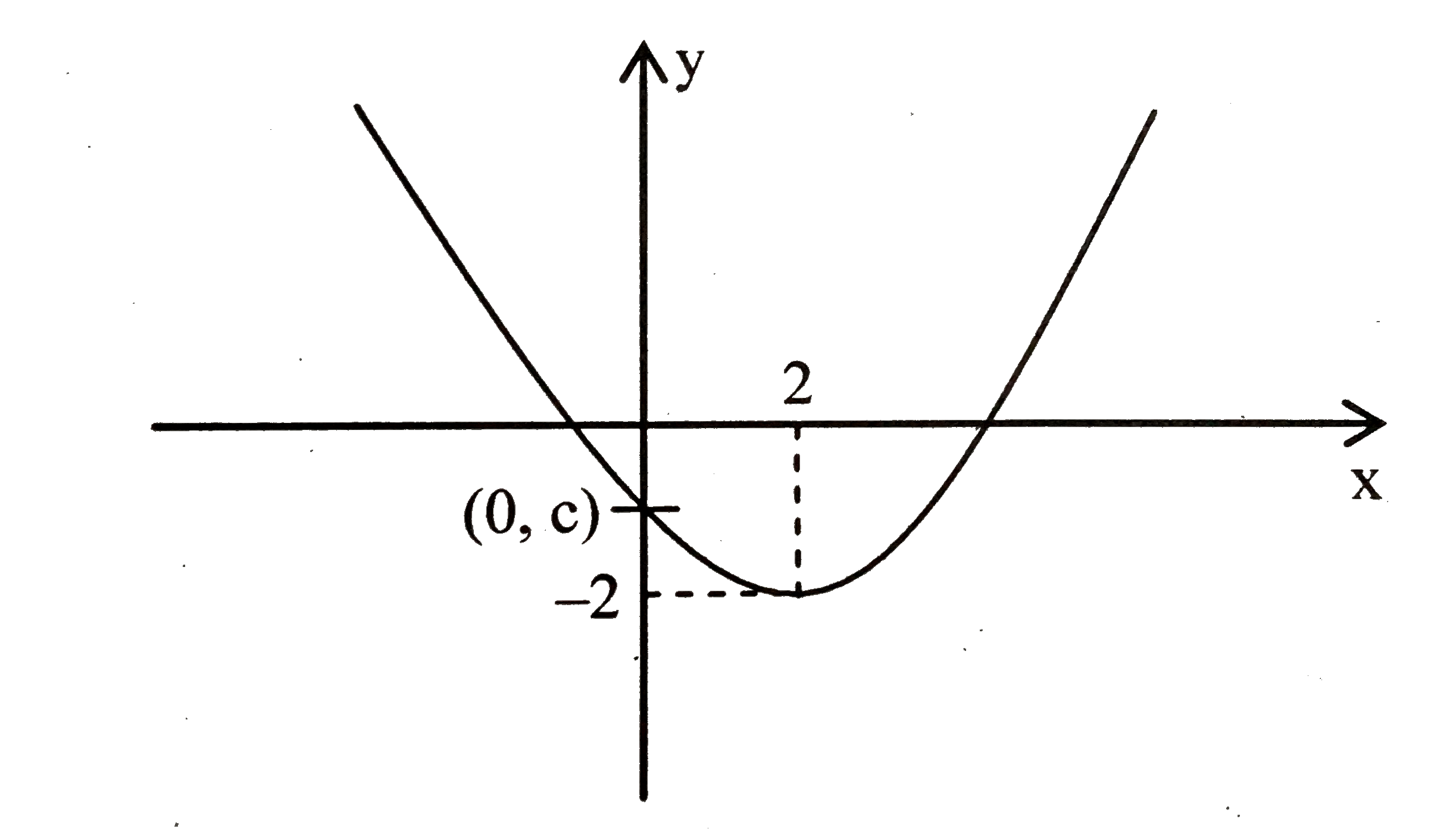
Suppose A Parabola Y Ax 2 Bx C Has Two X Intercepts One Pos
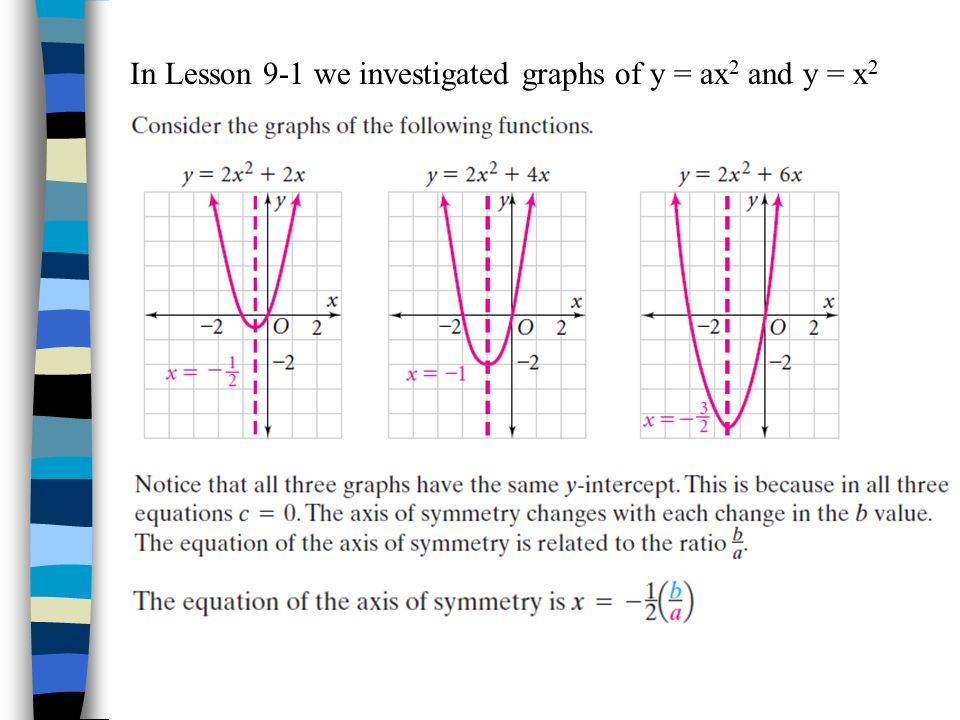
Lesson 9 2 Graphing Y Ax Bx C Objective To Graph Equations Of The Form F X Ax Bx C And Interpret These Graphs Ppt Download
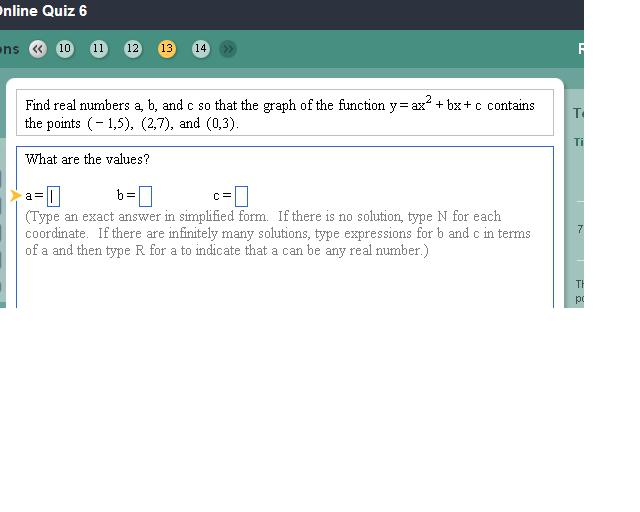
Solved Find Real Numbers A B And C So That The Graph Of Chegg Com

This Professor S Amazing Trick Makes Quadratic Equations Easier The New York Times

Solved In Y Ax 2 Bx C The X Coordinate Of The Verte Chegg Com

Let F X Ax 2 Bx C Consider The Given Diagram Then
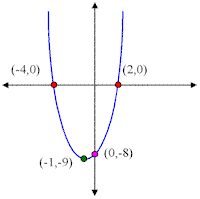
Parabolas
A Tangent To A Quadratic
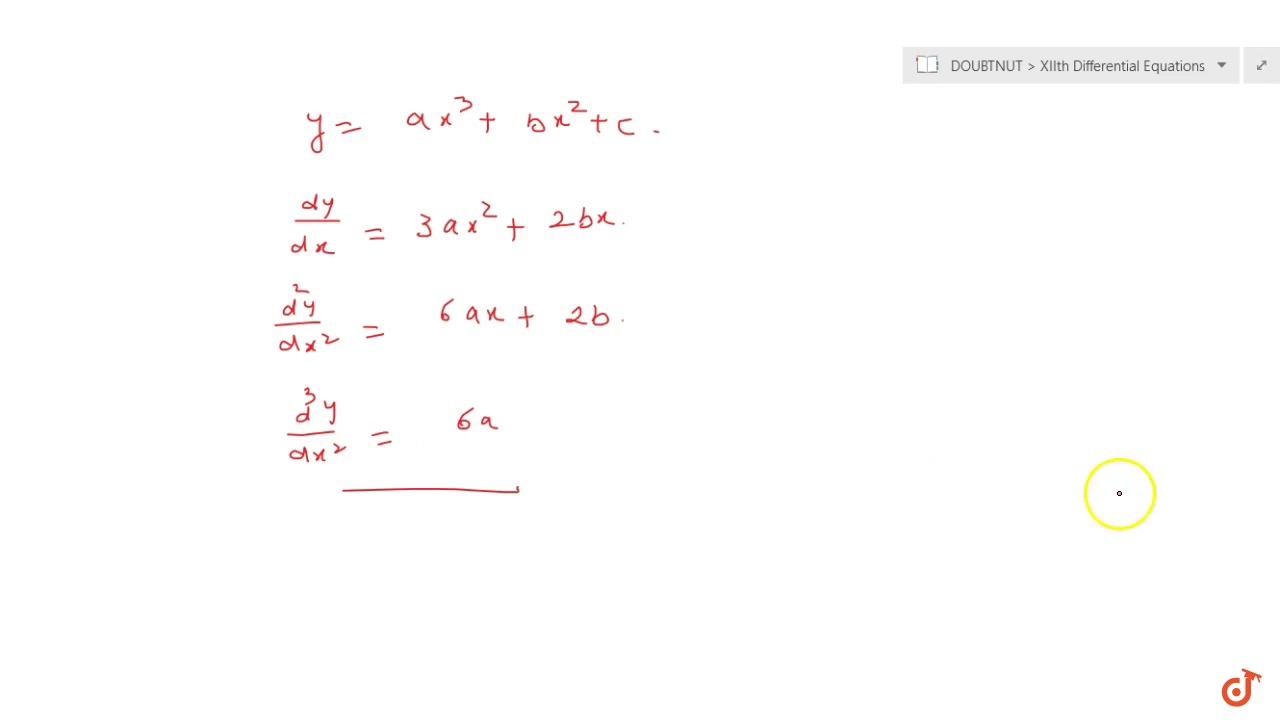
Show That Y A X 3 B X 2 C Is A Solution Of The Differential Equation D 3y Dx 3 6a Youtube
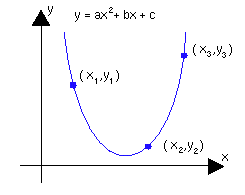
Linear Algebra Webnotes Class Assignments Chapter 1

Quadratic Function Wikipedia
Quadratic Functions
Assignment 2 Investigating The Relationship Between The Two Standard Forms Of The Graph Of A Parabola
Quadratic Equation Formulas Tricks For Solving Quadratic Equations
Exploring Parabolas Y Ax 2 Bx C

Graphing Y Ax 2 Bx C

Ch8 Quadratic Equation Solving Methods General Form Of Quadratic Equation Ax 2 Bx C 0 A Quadratic Equation X 2 7x 10 0a B Ppt Download

Example 3 Graph A Function Of The Form Y Ax 2 Bx C Graph Y 2x 2 8x 6 Solution Identify The Coefficients Of The Function The Coefficients Ppt Download
Q Tbn 3aand9gcskitjvtu4g6u7oh5r8z42jlb391urt3idlmfdbjguuxli7v2fo Usqp Cau
The Following Figure Shows The Graph Of F X Ax 2 Bx C Then
Pdf Key Concepts Of Quadratic Functions And Inequalities First Edition
If Ax Bx C 0 And A B C 0 What Would Be The Value S Of X Quora

Quadratic Formula Calculator
Ch 4 Pre Test 1 Graph The Function Y 4x 2 Then Label The Vertex And Axis Of Symmetry 2 Write The Quadratic Function In Standard Form Y X Ppt Download
The Graph Of Y Ax 2 Bx C Geogebra
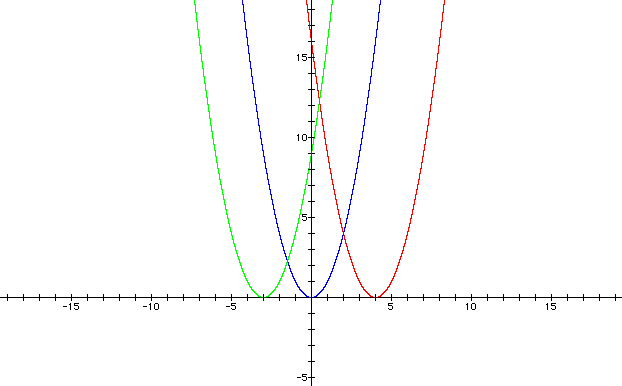
Solved Graphs Of The Following Three Equations Are Shown Chegg Com
Suppose A Parabola Y Ax 2 Bx C Has Two X Intercepts One Positive And One Negative And Its Vertex Is 2 2 Sarthaks Econnect Largest Online Education Community

Solved Use The Graph Of Y Ax2 Bx C To Solve A Quadr Chegg Com
Quadratic Function Wikipedia
Solved The Curve Y Ax 2 Bx C Passes Through The Poi Chegg Com

Quadratic Function Wikiwand
Graph Of A Quadratic Function

2 Graph Of Y Ax 2 Bx K Graph Of Y Mx K Download Scientific Diagram
Parabolas

B Value Definition Explanation Video Lesson Transcript Study Com
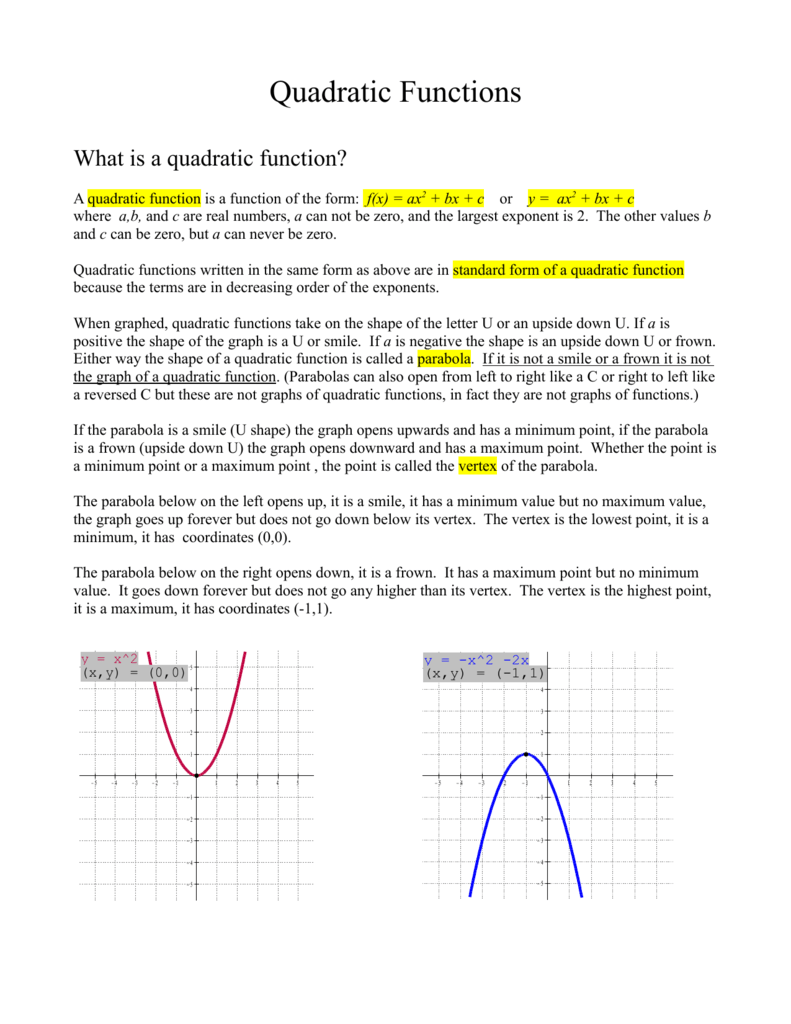
Quadratic Functions
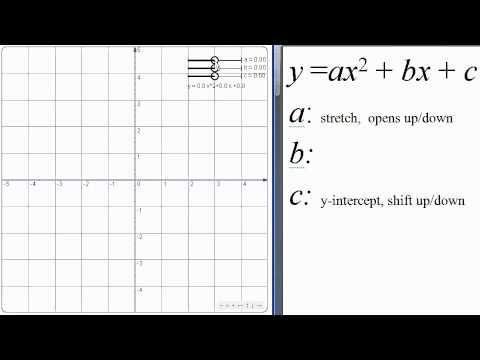
Effect Of A B C On Quadratic Youtube
The Graph Of Y Ax 2 Bx C Has A Minimum At 5 3 And Passes Through 4 0 How Do I Find The Values Of A B And C Quora
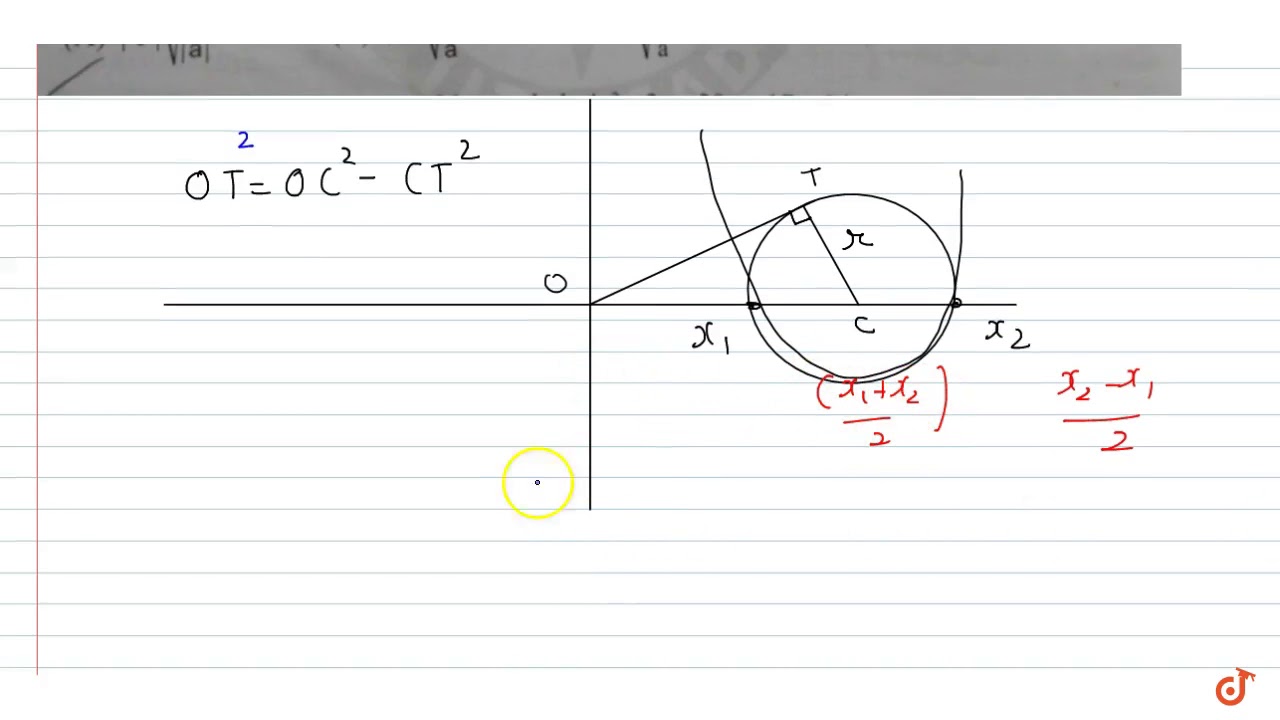
A Parabola Y Ax 2 Bx C Ac Gt 0 Crosses The X Axis At A And B A Variable Circle Is Dra Youtube
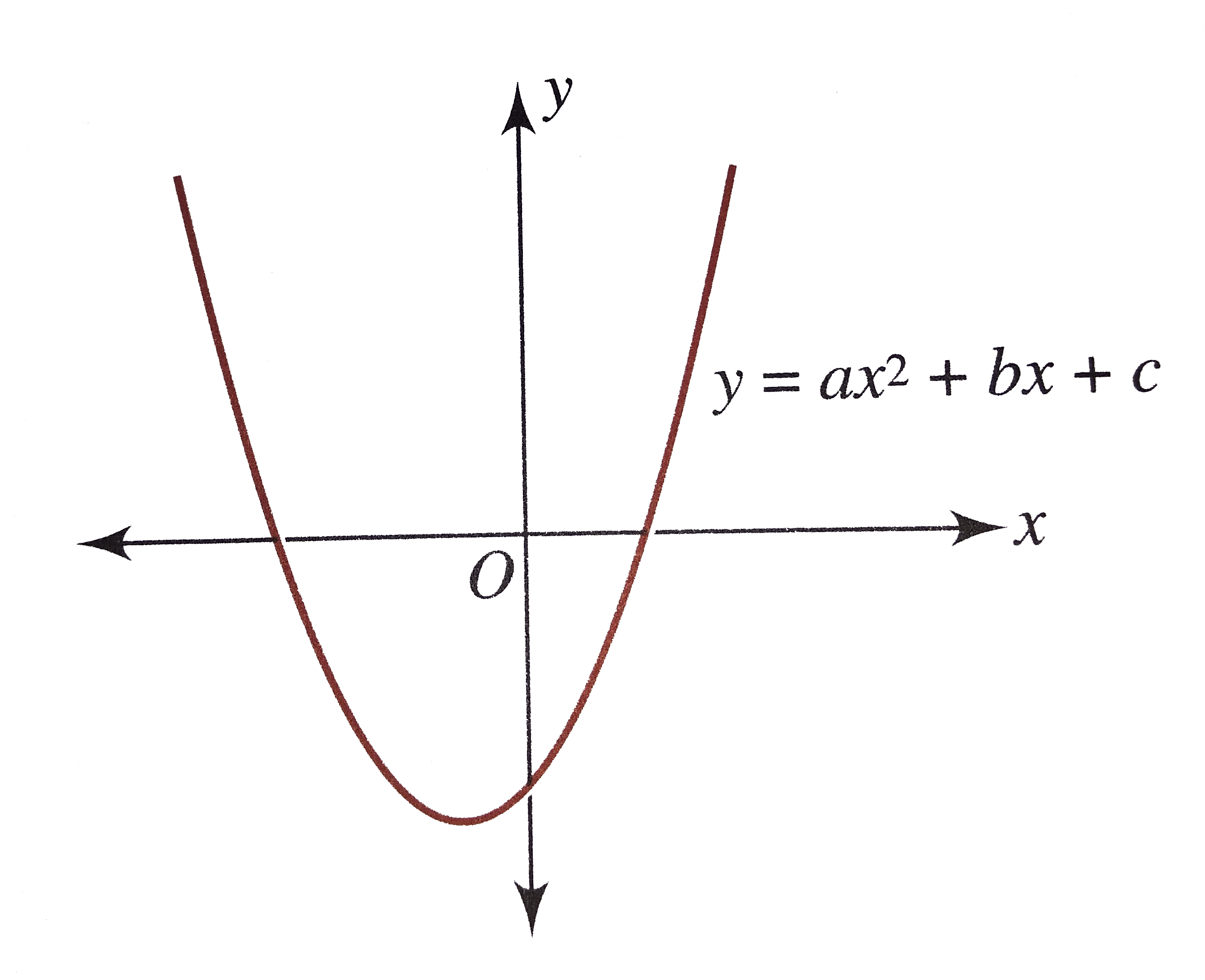
The Following Figure Shows The Graph Of F X Ax 2 Bx C Then

Y Ax2 Bx C Quadratic Function Quadratic Term Linear Term Ppt Download
Graphing Quadratic Functions
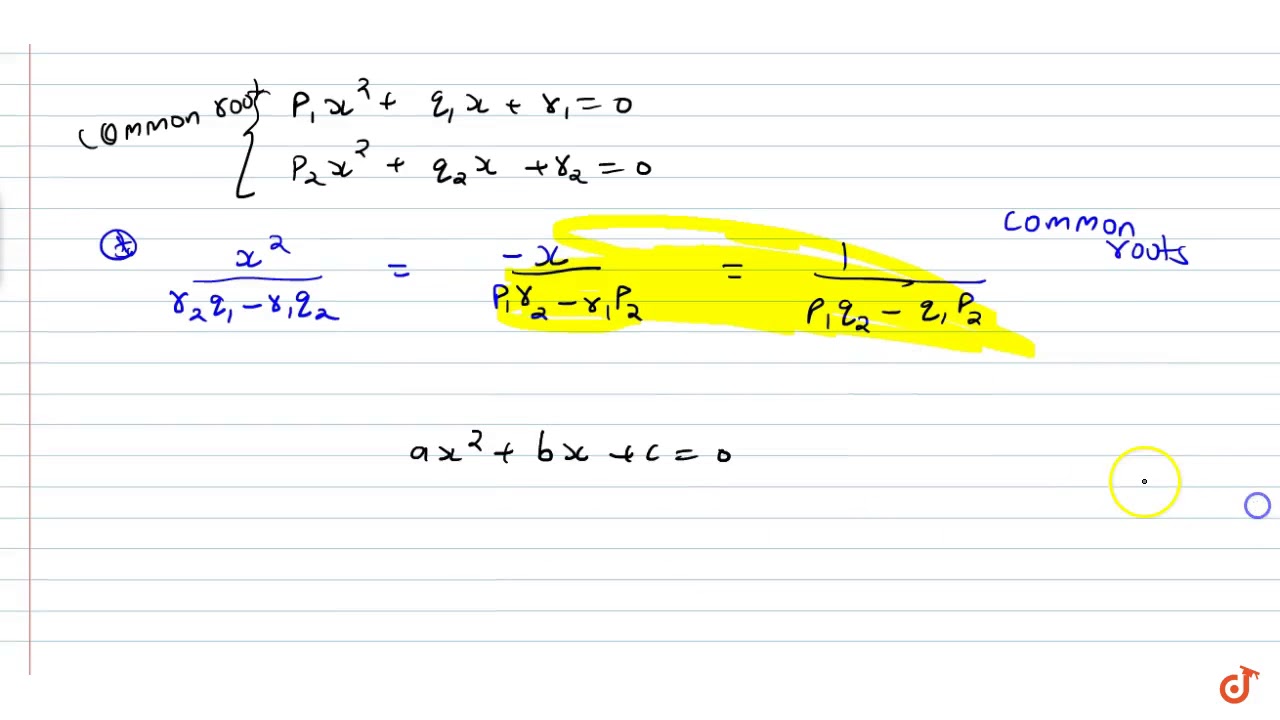
If Ax 2 Bx C 0 And Bx 2 Cx A 0 Have A Common Root And A 0 Then A 3 B 3 C 3 Ab Youtube

Graphing Y Ax2 Bx C Youtube

If The Diagram In Fig 2 22 Shows The Graph Of The Polynomial F X Ax Bx C Then A A Gt 0 Brainly In
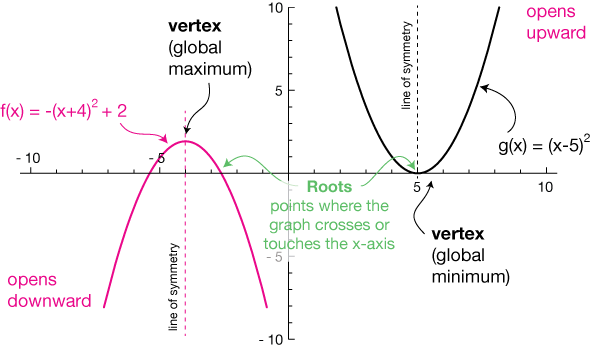
Quadratic Functions
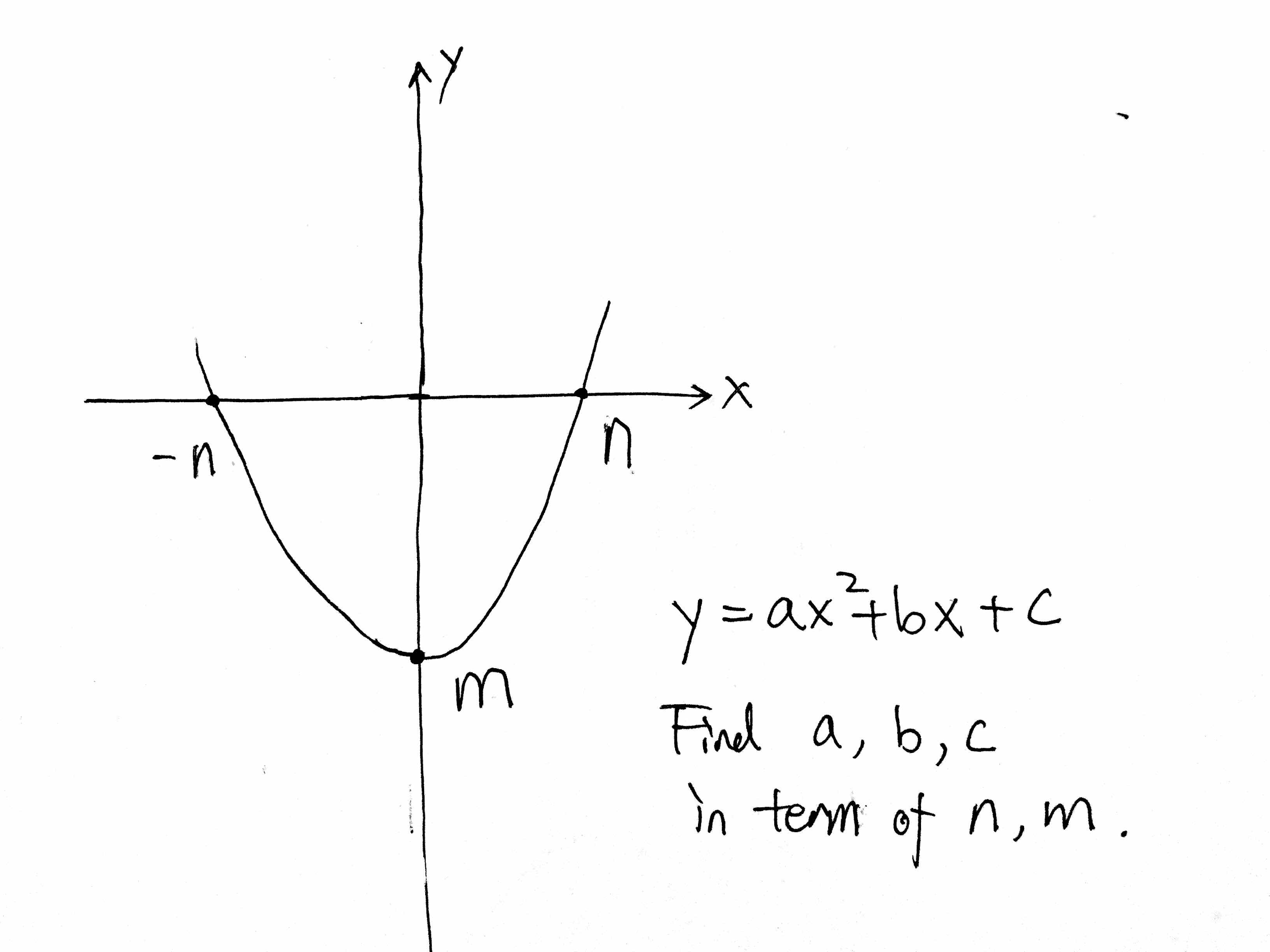
Solved Y Ax 2 Bx C Find A B C In Term Of N M Chegg Com

The Graph Of The Quadratic Function Y Ax 2 Bx C Is Given Find A B C Brainly Com
Math Spoken Here About Quadratics 3
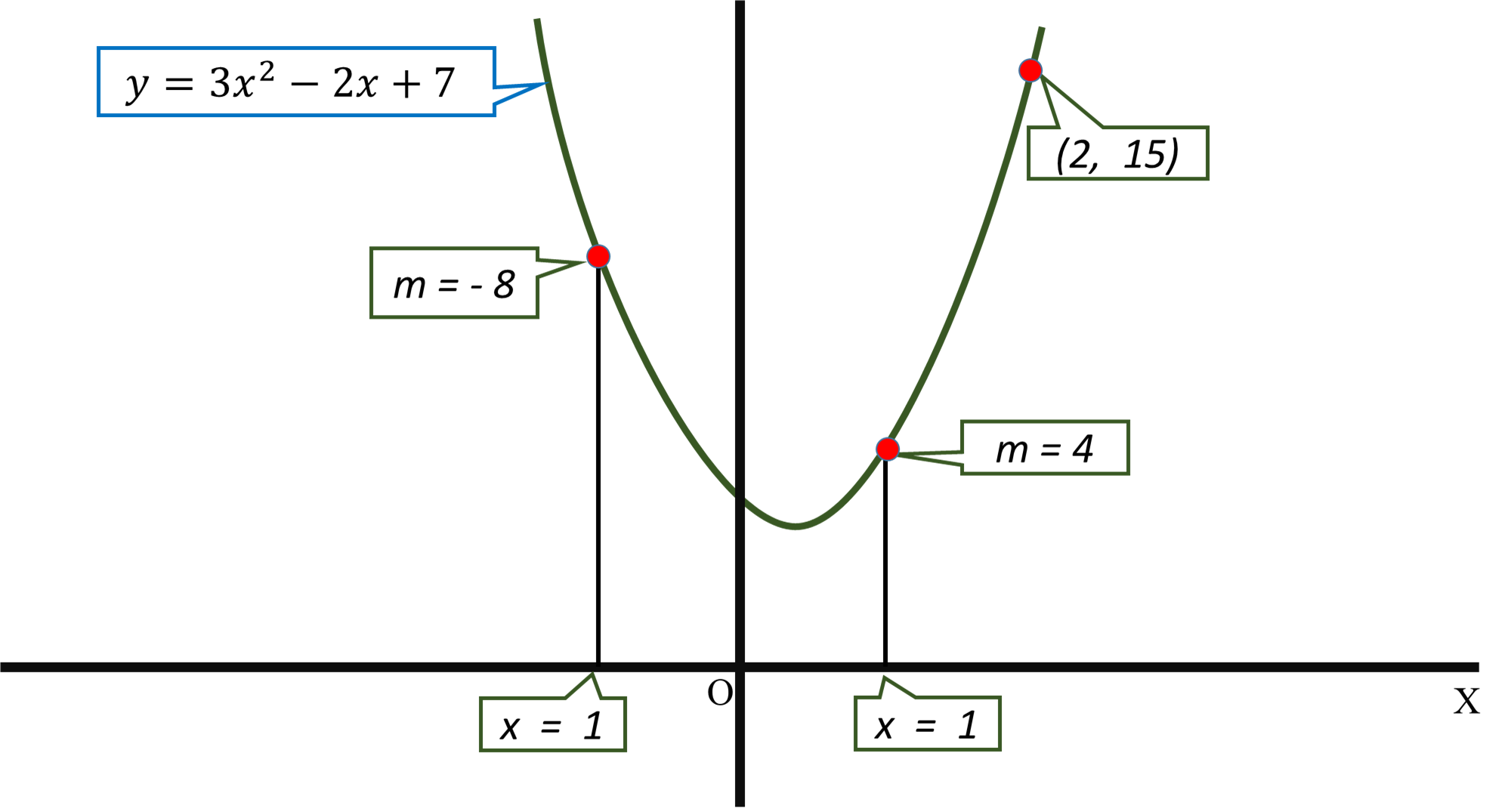
How Do You Find A Parabola With Equation Y Ax 2 Bx C That Has Slope 4 At X 1 Slope 8 At X 1 And Passes Through 2 15 Socratic

To Investigate The Effect Of The Constants A B And C On The Graph Y Ax2 Bx C Gcse Maths Marked By Teachers Com

To Investigate The Effect Of The Constants A B And C On The Graph Y Ax2 Bx C Gcse Maths Marked By Teachers Com
The Graph Of Y Ax 2 Bx C Algebra 1 Quadratic Equations Mathplanet
The Graph Of Y Ax 2 Bx C Algebra 1 Quadratic Equations Mathplanet
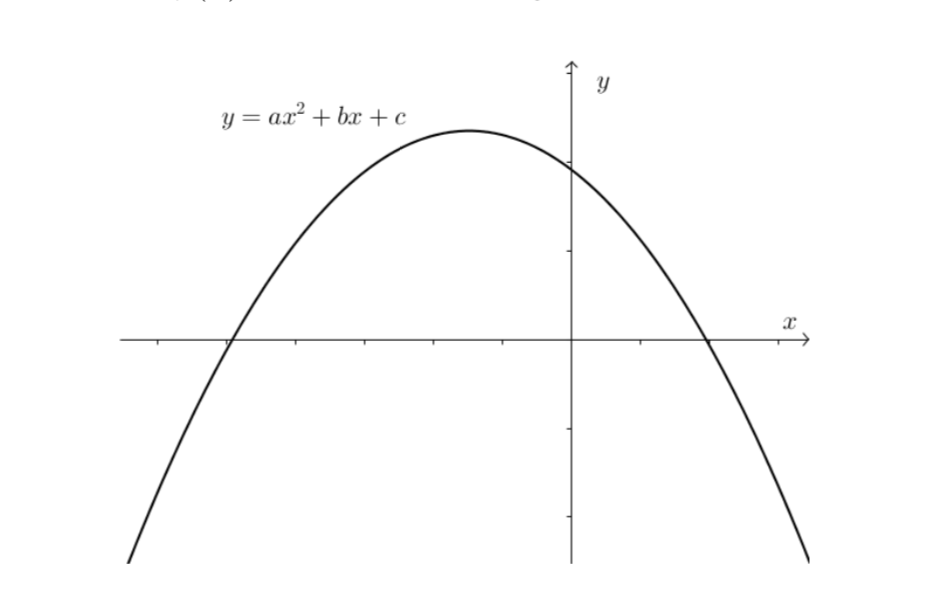
Solved The Graph Of A Quadratic Function F X Ax2 Bx Chegg Com

The Graphs Of Y Ax 2 Bx C Are Given In Figure Identify The Signs Of A B And C In Each Of The Following

The Parabola Y Ax 2 Bx C Is Graphed Below Find A B C The Grid Lines Are One Unit Brainly Com

Ch 4 Pre Test 1 Graph The Function Y 4x 2 Then Label The Vertex And Axis Of Symmetry 2 Write The Quadratic Function In Standard Form Y X Ppt Download

Solved The Equation For A Parabola Has The Form Y Ax 2 Chegg Com

Quadratic Equation Wikipedia

Correlation Coefficients R And Coefficients A B And C Of The Linear Download Table
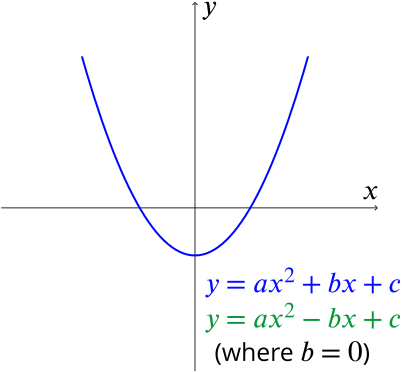
Solution Discriminating Quadratics Underground Mathematics

Math Spoken Here About Quadratics 3

Assignment 2

Ex Write Ax 2 Bx C In The Form A X H 2 K Negative A Youtube
Braingenie Graphing Y Ax Sup 2 Sup Bx C Using A Table Of Values

How To Solve A Quadratic Equation How To Excel
Quadratic Function Finding The Solutions Roots Of A Quadratic Function By Graphing Ppt Download
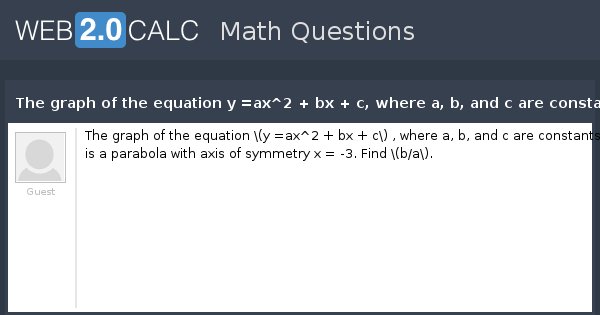
View Question The Graph Of The Equation Y Ax 2 Bx C Where A B And C Are Constants Is A Parabola With Axis Of Symmetry X 3 Find B A
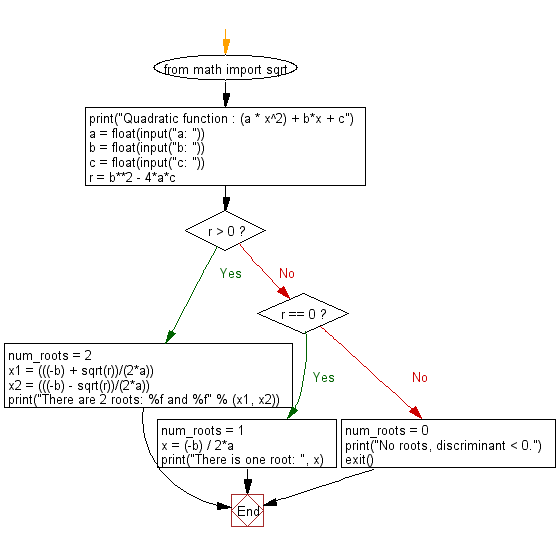
Python Math Find The Roots Of A Quadratic Function W3resource

Find The Sign Of A B C In Ax 2 Bx C Given The Graph And A Coordinate On It Mathematics Stack Exchange

Quadratic Formula Wikipedia
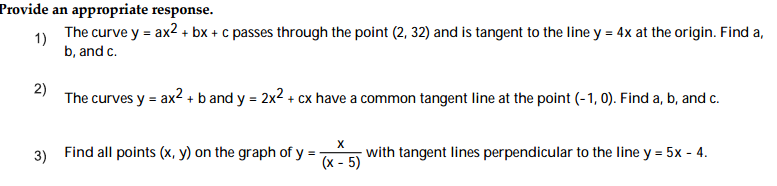
Solved Provide An Appropriate Response 1 The Curve Y Chegg Com
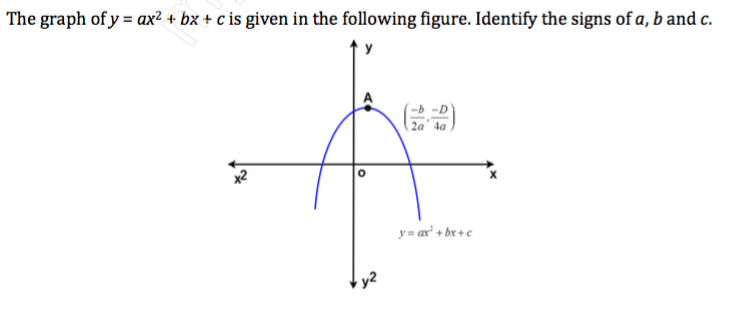
Solved The Graph Of Y Ax 2 Bx C Is Given In The Fol Chegg Com

B Value Definition Explanation Video Lesson Transcript Study Com
Q Tbn 3aand9gcskitjvtu4g6u7oh5r8z42jlb391urt3idlmfdbjguuxli7v2fo Usqp Cau
Quadratic Functions The Effect Of B Geogebra
Q Tbn 3aand9gcryrqqkv5cqqc2yszh6lmsoozxbkej1joyujwh0lecbpgvkm9nx Usqp Cau

Consider The Graph Of Quadratic Polynomial Y Ax 2 Bx C As Shown Below Which Of The Following Is Are Correct
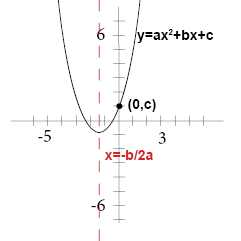
The Graph Of Y Ax 2 Bx C Algebra 1 Quadratic Equations Mathplanet
Quadratic Equation Wikiwand

Quadratic Function Wikiwand

The Expression Y Ax 2 Bx C Has Always The Same Sign As Of A If A 4ac Lt B 2 B 4ac Youtube

Graphing Parabolas
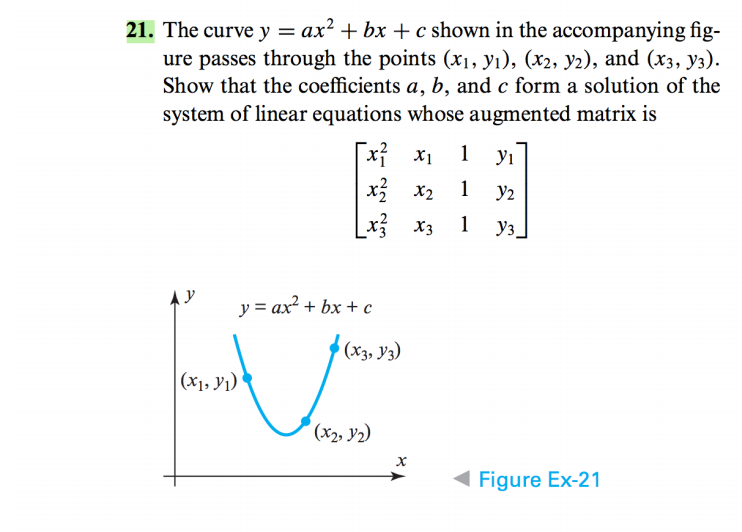
Solved The Curve Y Ax 2 Bx C Shown In The Accompany Chegg Com
Graphing Quadratic Functions Ppt Video Online Download
Quadratic Relations Y Ax 2 Bx C Between The A N B P And Download Scientific Diagram

The Given Figure Shows The Graph Of The Polynomial F X Ax 2 Bx C Then Ltbr Gt 1 Nbsp Youtube
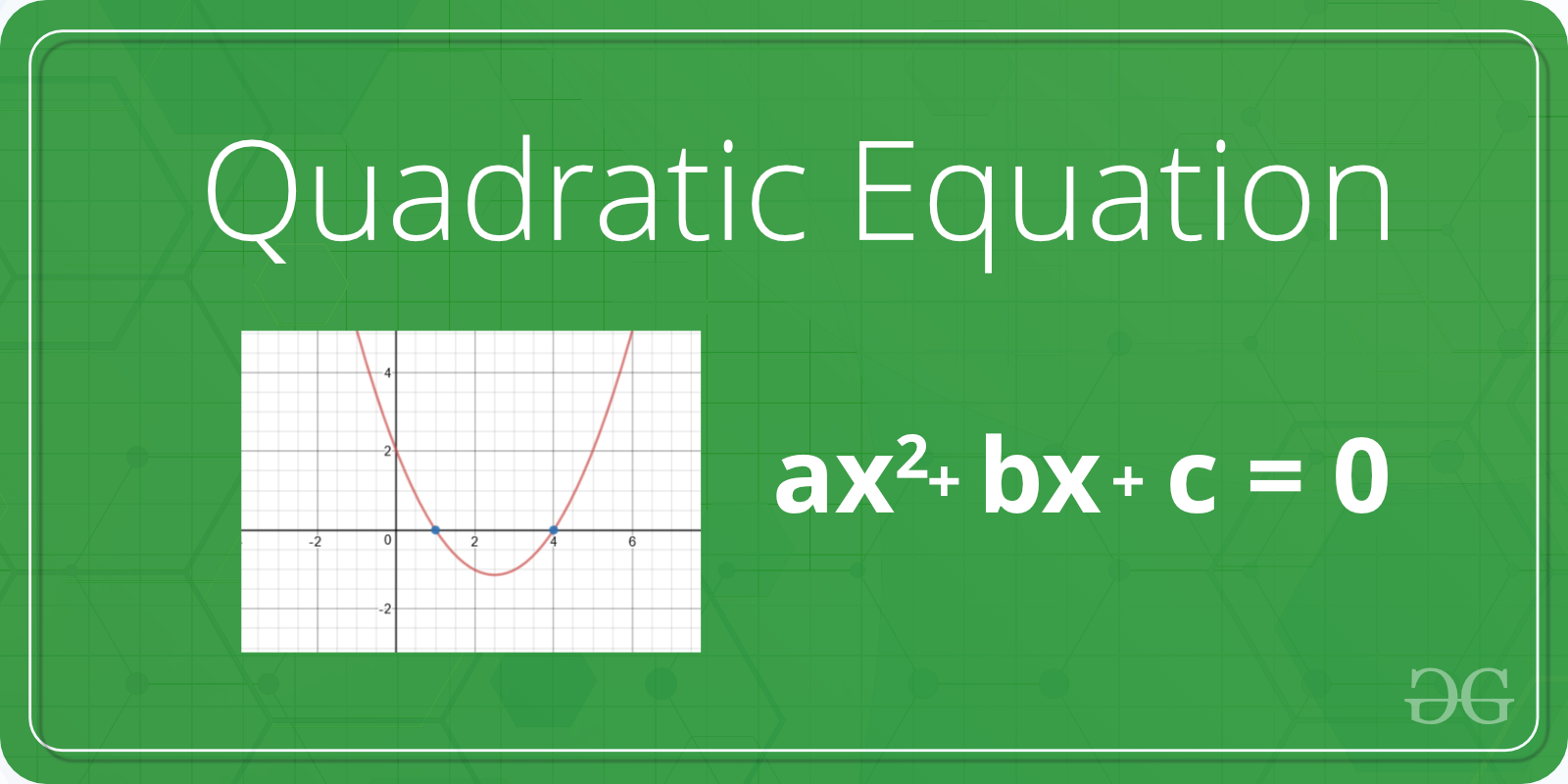
Program To Find The Roots Of Quadratic Equation Geeksforgeeks
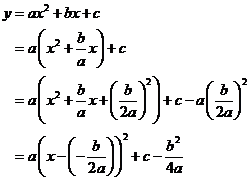
Assignment 2 Investigating The Relationship Between The Two Standard Forms Of The Graph Of A Parabola
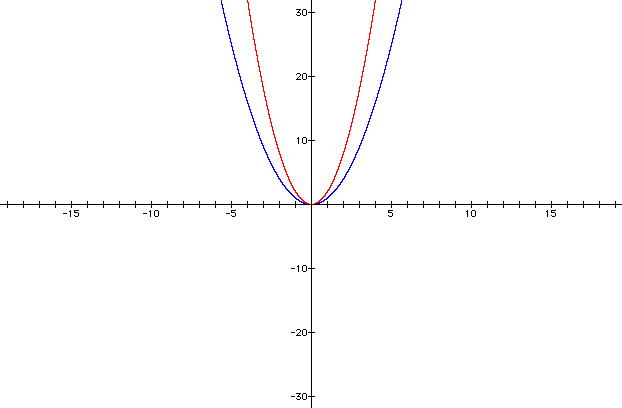
Graphing Quadratic Functions

If The Diagram Given Below Shows The Graph Of Thepolynomial F X Ax 2 Bx C Then

Ch8 Quadratic Equation Solving Methods General Form Of Quadratic Equation Ax 2 Bx C 0 A Quadratic Equation X 2 7x 10 0a B Ppt Download
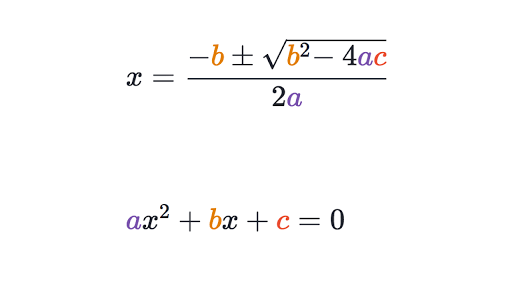
Quadratic Formula Proof Review Article Khan Academy
Equations And Graphs

Gmat Club Forum Given That F X Ax 2 B X C And F X Y F X F Y Xy For Problem Solving Ps



